Discover the best LLM of world math problems solutions on our blog for expert insights and strategies to tackle challenging math problems.
Key Highlights
Role of LLMs in Complex Math: LLMs simplify math by interpreting problems naturally, generating solutions, and assisting with advanced challenges, making them versatile from basic calculations to research.
Key Features for Math Problems: LLMs convert word problems into equations, offer multiple strategies, perform error checking, combining speed and accuracy for effective problem-solving.
Top LLMs Comparison: GPT-4, LLaMA 3.1 405B, and Claude 3.5 excel in different areas. LLaMA 3.1 leads in performance and cost-effectiveness, while GPT-4 offers diverse approaches to complex math.
Real-world Applications: LLMs are transforming industries, speeding up problem-solving in AI, research, and education by analyzing data, validating solutions, and uncovering new insights.
Boosting Efficiency with Novita AI: Novita AI’s LLM API, like LLaMA 3.1 and Gemma-2–9b-it, enhances math problem-solving by providing accurate solutions and automating tasks, improving productivity.
Future of LLMs in Math: LLMs will play a key role in future math advancements, driving research, personalized learning, and automation of complex tasks across various industries.
Introduction
In the early days of math problem-solving, solutions relied on manual calculations, established rules, or specialized software. However, the rise of LLMs has simplified this process by leveraging natural language understanding to tackle even the most complex mathematical problems. LLMs simplify math by providing step-by-step explanations and diverse problem-solving strategies, making them an invaluable tool for students, researchers, and professionals. With advancements in AI, platforms like Novita AI are offering powerful LLM API that enhances math efficiency and accuracy across various tasks.
The Role of LLM in Solving Complex Math Problems
Traditionally, math problem-solving relied on rules or specialized software. Language models (LLMs) take a unique approach by leveraging their language understanding to solve math problems naturally. This ability simplifies math for all and enables collaboration with AI on complex challenges. Moreover, LLMs continuously improve, making them ideal for various math tasks, from everyday calculations to cutting-edge research.
Understanding the Importance of LLM in Mathematics
Large language models play a crucial role in math by finding the correct answers and processing and simplifying complex math ideas. They aid in explaining solutions clearly, making learning challenging topics easier for students. Moreover, these models assist in theorem proving and mathematical research by analyzing theorems, identifying patterns, and suggesting innovative ideas to advance mathematical knowledge. The combination of human intellect and large language model capabilities presents exciting possibilities for tackling difficult problems and uncovering significant discoveries in mathematics.
How LLMs Have Transformed Math Problem Solving
Understanding and Interpreting Problems: LLMs can parse complex mathematical language and identify key components of a problem, such as variables, equations, and constraints. This ability enables them to provide accurate interpretations and insights.
Step-by-Step Solutions: LLMs can generate solutions to mathematical problems, breaking down intricate concepts into manageable parts. This pedagogical approach aids in understanding and learning.
Diverse Problem-Solving Strategies: LLMs are trained on a vast array of mathematical techniques and strategies. They can suggest multiple approaches to a problem, allowing users to choose the most suitable method.
Error Checking and Validation: By providing solutions, LLMs can also help identify errors in reasoning or calculation. They can validate solutions by checking against established mathematical principles.
Accessibility and Learning: LLMs make complex mathematics more accessible to a broader audience, including students and non-experts. They can provide explanations in simpler terms, enhancing understanding.
Key Features of LLMs in Addressing World Math Problems
LLMs excel at solving various math problems by converting complex word problems into mathematical equations through their natural language understanding. They leverage vast information, including theorems, formulas, and real-world data, to approach problems from different angles.
Speed and Efficiency
LLMs excel at problem-solving with their neural network design, processing information rapidly. They explore multiple strategies simultaneously to identify the best solution swiftly. Their efficiency has broad implications, enabling quick analysis of vast datasets and hypothesis testing. Leveraging LLMs’ speed in addressing mathematical challenges can help businesses improve operations and make data-driven decisions for a competitive edge.
Accuracy Across Different Math Domains
Large language models excel in basic math like arithmetic, algebra, and basic calculus but struggle with advanced topics such as advanced calculus, abstract algebra, and number theory. They perform well in simpler math but fall short in complex math due to the need for deeper understanding, logical reasoning, and creative problem-solving. More research is needed to improve their accuracy in intricate math fields through specialized training data and enhanced ability to handle complex concepts using symbolic reasoning systems.
Best LLM of World Math Problems: Leading LLMs Comparison
Next, we will compare three major models: GPT-4, LLaMA 3.1 405B, and Claude 3.5. This comparison will show how each model deals with math challenges. We will also look at what they can do well and where they can improve.
Models Overview
GPT-4
Chat GPT-4, the latest version of OpenAI’s Generative Pre-trained Transformer, excels at solving math problems. It offers multiple solutions for a given problem, allowing users to choose the best approach. Trained on a vast dataset encompassing code, text, and mathematical expressions, GPT-4 can tackle complex problems.
LLaMA 3.1 405B
LLaMA 3.1 405B, a large language model by Meta, is known for its exceptional math skills with 405 billion parameters. It excels in symbolic manipulation, handling algebra, equations, and calculus effortlessly. Ideal for students, teachers, and researchers, it demonstrates a strong grasp of math structures and logical reasoning to solve complex problems.
Claude 3.5
Claude 3.5, the latest model from Anthropic in the LLM field, uniquely solves math problems while prioritizing human values and intentions. It focuses on providing correct and easily understandable answers, making it ideal for educational purposes.
Math Performance Comparison
In this section, we will compare these models with the benchmark related to math performance.
In LLM evaluation, GSM8K is a dataset of 8,000 grade-school math word problems. Testing a large language model’s mathematical reasoning involves multi-step problems with basic arithmetic operations like addition. These problems include elementary arithmetic (+ − ×÷) and typically require 2 to 8 steps to solve.
MathEval is the initial all-in-one LLM benchmark designed to evaluate mathematical skills comprehensively in LLMs.
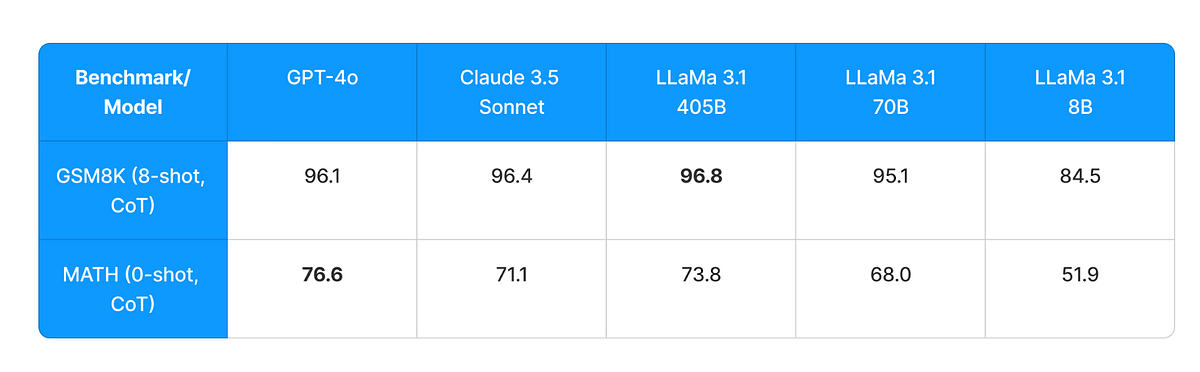
Through the benchmark in the graph, we can see that Llama 3.1 405B outperform other models in GSM8K and slightly inferior to GPT-4o. But look at the price, Llama 3.1 405B is much more cost-effective than GPT-4o.
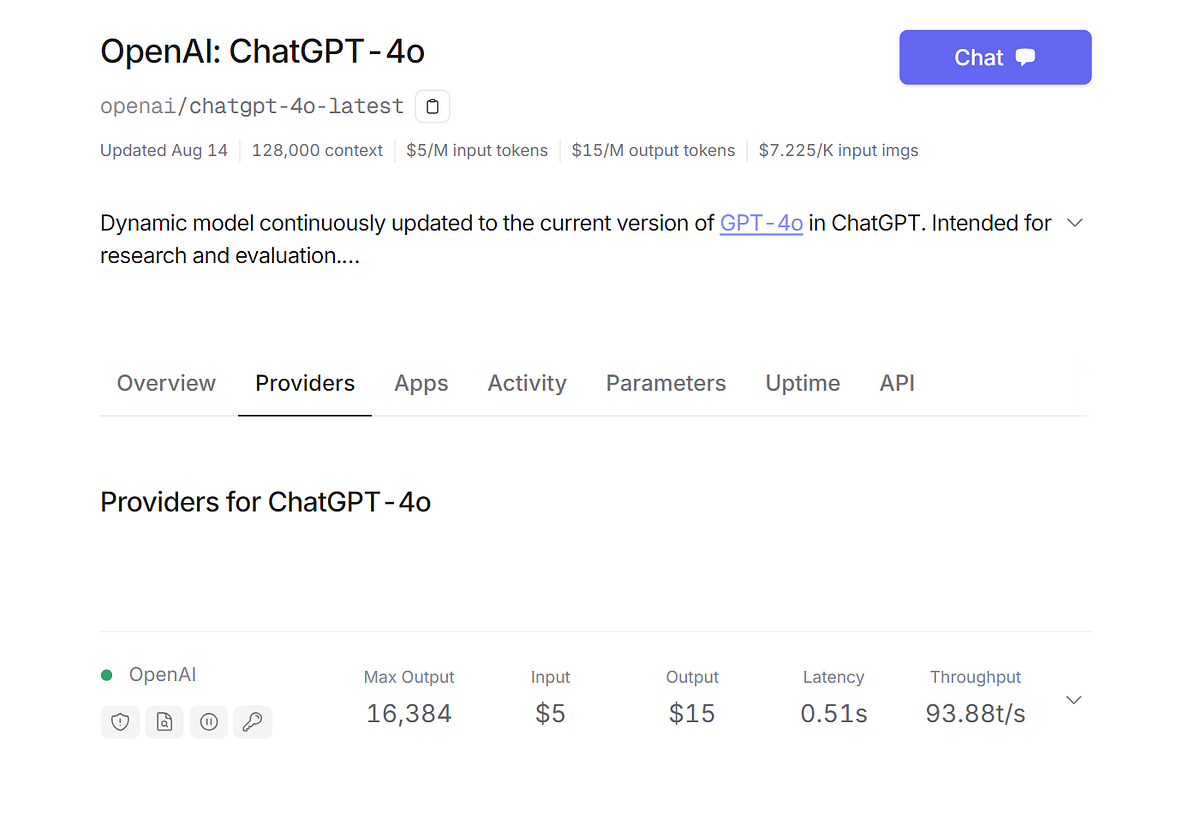
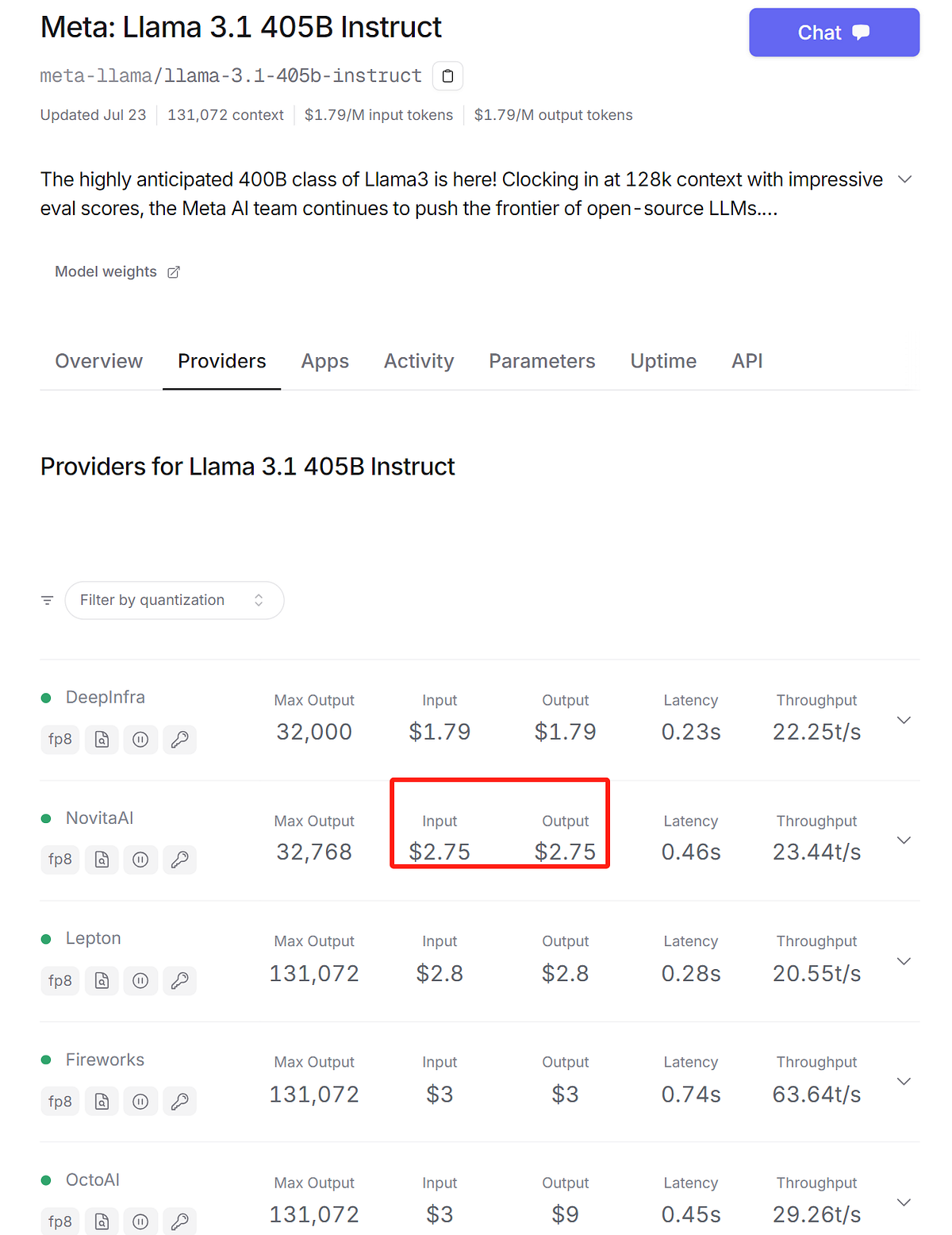
Now Novita AI cut the price of Llama 3.1 405B to only $2.75 for input/output per million tokens.
Real-world Applications of LLMs in Solving Math Problems
The great abilities of LLMs in solving math problems have made them useful in many real-world areas. Here are some examples.
How LLMs Are Being Used in the AI Industry
LLMs, or Large Language Models, are transforming the AI industry. These models undergo rigorous testing to ensure accuracy and efficiency in processing natural language. Tech enthusiasts share insights on social media like YouTube about LLMs’ potential applications and impact across sectors. As AI research evolves, LLMs will shape technology’s future and redefine human-machine interactions. Continued exploration of these models is crucial for driving AI advancements in the digital landscape.
LLMs in Academic Research: Breaking New Ground
LLMs revolutionize academic research by speeding up discovery and solving complex problems. In physics and astronomy, they analyze data to uncover patterns and anomalies for new insights about the universe. In climate science, LLMs predict weather patterns, assess climate impacts, and aid in developing solutions. They are not just tools but active collaborators in exploration, with more breakthroughs expected as LLM technology advances.
Public Perception and Acceptance of LLMs in Math Education
Public opinion and acceptance of LLMs in math education are crucial. While concerns exist about technology’s impact on learning and the role of LLMs versus human teachers, viewing LLMs as tools that enhance learning is essential. When used wisely, LLMs can personalize lessons, offer prompt feedback, and enable teachers to focus on individual student needs. Effective communication among teachers, parents, and decision-makers is vital to ensure the safe and ethical use of LLMs in schools. Building trust through transparency promotes wider acceptance and effective utilization of LLMs in math education. You can view more about people’s attitudes toward AI math education on TikTok.
How to Elevate Your Efficiency in Math Problems: LLM API
Solving complex math problems can often be time-consuming, requiring deep analysis and numerous calculations. Using an LLM API like Novita AI, you can simplify mathematical tasks and enhance accuracy.
Why Novita AI?
Novita AI is at the forefront of offering cutting-edge LLMs that cater to a diverse set of use cases, including mathematics.
Our platform is tailored for developers who want reliable, scalable, and high-performance LLMs to reach more than limited users.
By using Novita AI, you get access to powerful models and benefit from a supportive ecosystem designed to boost your productivity and efficiency in problem-solving without minimal incorrect answers.
You can get timely support at the Novita AI discord community.
Step-by-step Guide Using Novita AI LLM API
Harnessing the power of Novita AI’s LLM API can significantly enhance your problem-solving capabilities in math. Here’s a step-by-step guide to get started with high LLM performance:
Step 1. Sign up on Novita AI: Head over to the Novita AI platform and create an account if you visit our website for the first time. Once you’re in, you’ll have access to various LLM models designed to meet your needs.
Step 2. Explore Available Models: Novita AI offers a range of LLMs, each with specific strengths. For math-related tasks, choose a model optimized for reasoning and computation, such as Llama 3.1 series or Gemma-2–9b-it.
Here is a sample using Gemma-2–9b-it to solve math problems. You can explore more on Novita AI LLM Playground.
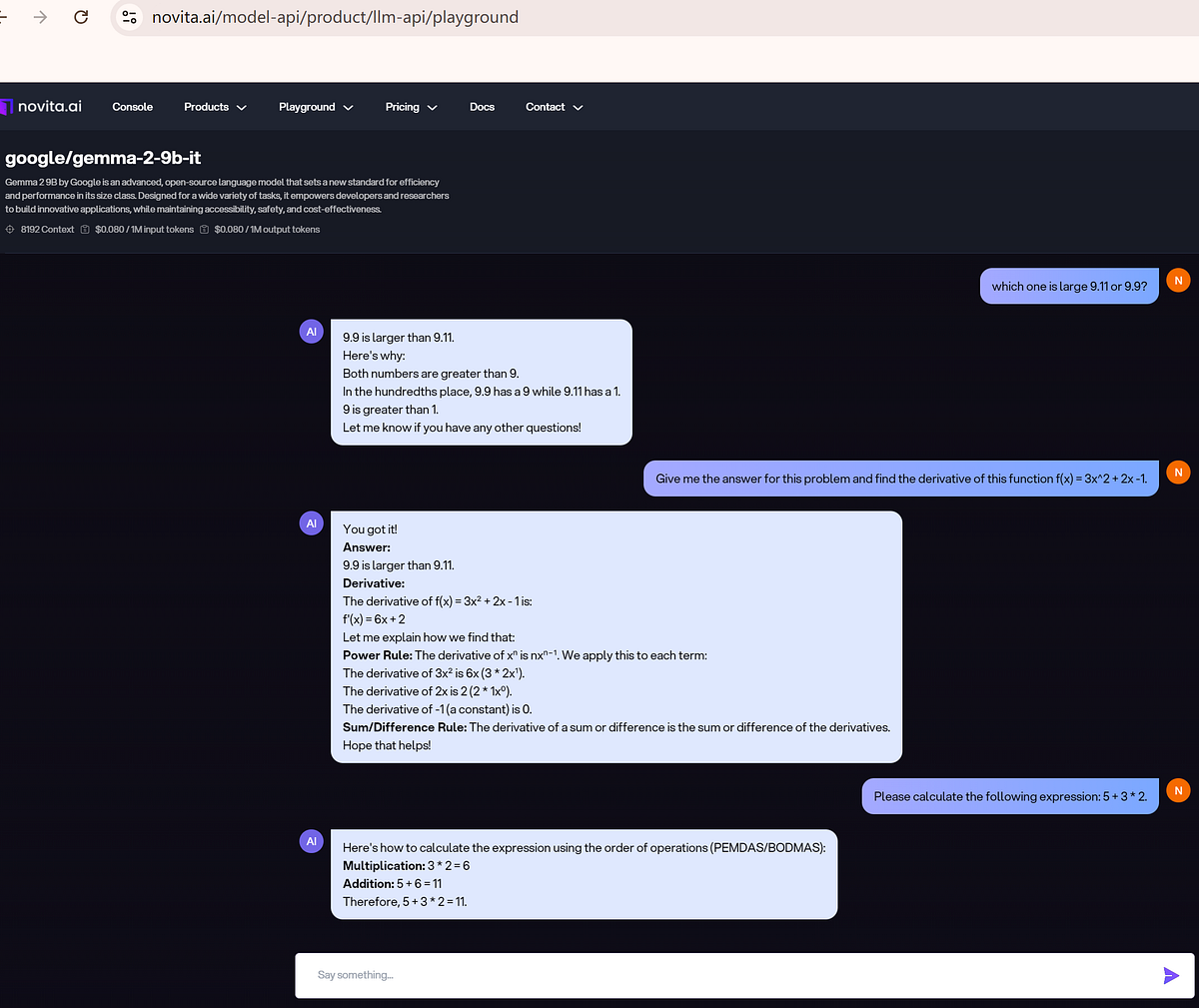
- Step 3. Access the API Documentation: Obtain your API key in Novita AI Key management. Novita AI provides comprehensive API documentation that allows you to integrate their LLM into your application or workflow seamlessly. It includes detailed instructions on how to input your mathematical queries.
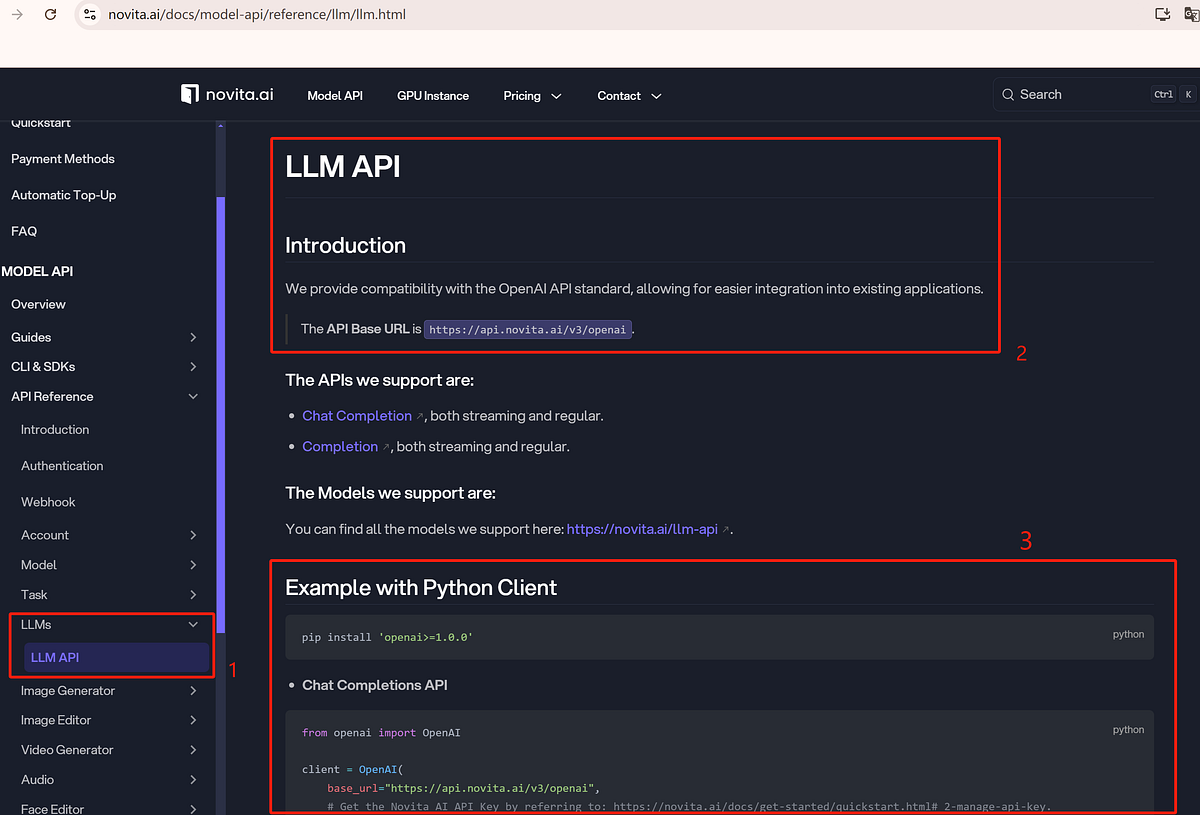
Step 4. Send a Query: Use the API to input your math problem. Whether it’s solving equations, finding derivatives, or even performing advanced matrix operations, the API can break down the problem and return a step-by-step solution in seconds.
Step 5. Analyze the Response: The LLM will provide an answer and explain the solution, helping you understand the reasoning process and ensuring accuracy.
Step 6. Iterate and Solve More Problems: Once familiar with the process, you can automate repetitive calculations or tackle even more complex math problems to get the final answer.
The Future of LLMs in Mathematics
The future of LLMs in math is promising. These models will revolutionize math research, education, and problem-solving industries by tackling complex equations and enhancing human comprehension unexpectedly.
Emerging Trends in LLM Technology for Math
LLM technology for math is evolving rapidly. Models are being developed for multimodal reasoning, combining text, equations, and diagrams to solve complex problems in physics and engineering.
Another focus is on creating LLMs that provide detailed explanations for their answers, enhancing transparency.
Exploring quantum-enhanced LLMs that leverage quantum computing for problem-solving could change cryptography and drug discovery.
Predictions for Future LLM Developments in Math Solutions
In the future, LLMs in math solutions will offer personalized tutors that adapt to each student’s learning style, potentially revolutionizing math education to make it more engaging and accessible.
LLMs automate mathematical research, helping mathematicians explore new concepts, verify proofs, and uncover mathematical relationships.
LLMs will use real-time data to solve problems, forecast markets, and manage logistics.
Conclusion
In conclusion, LLMs have changed math problem-solving. They offer speed and accuracy, which greatly impacts education and research. Advanced models like GPT-4, LLaMA 3.1 405B, and Claude 3.5 are leading us towards a future where designing algorithms and AI ethics are important for math solutions. There are challenges ahead, but LLMs have endless possibilities in real-world uses across many fields. As we adapt to the new LLM technology, using these models in math education brings new chances and challenges. It shows that we need good plans to make the most of their ability to change learning in the classroom.
FAQs
What Makes LLMs Particularly Suited for Solving Math Problems?
They can understand natural language, which helps them solve word problems. This skill lets them convert the problems into a format that works for math. Also, they can quickly sort through a lot of information.
How Do GPT-4, LLaMA 3.1 405B, and Claude 3.5 Differ in Their Approach to Math?
GPT-4 is great at creative ideas and can explain why it makes those choices. LLaMA 3.1 405B is skilled at symbols and understanding math problems. Claude 3.5 focuses on safety and ethics.
Can LLMs Replace Traditional Methods of Learning and Solving Math Problems?
Although LLMs excel in certain mathematical reasoning tasks, they struggle with longer contextual information to solve more complex mathematical problems.
What Are the Ethical Considerations of Using LLMs in Math Problem Solving?
LLM’s output can benefit education, but ethical considerations like transparency need to be handled carefully to ensure that these technologies do not harm its fairness and effectiveness.
Originally published at Novita AI
Novita AI is the All-in-one cloud platform that empowers your AI ambitions. Integrated APIs, serverless, GPU Instance — the cost-effective tools you need. Eliminate infrastructure, start free, and make your AI vision a reality.

